I apologize for the lengthy surprise interruption of posts at The Retirement Cafe. The disruption was the result of personal issues that are now largely resolved, so I can resume blogging. I will, however, be changing the focus of the posts somewhat.
Previously, Retirement Cafe posts focused almost exclusively on retirement planning issues. Now that I have reached a later phase of retirement that began in 2005, I am experiencing a lot of practical issues related to my retirement strategy that I didn't quite foresee.
For example, I should have created backup options for my Two-Step Authentication-protected accounts to prepare for a lost or new phone. This is fairly easy to do in advance but a little harder in an emergency. I'll explain this in a separate post shortly.
A little planning and groundwork can simplify these activities and are best done before an emergency to save time and effort. I will be addressing these processes in future posts. I hope you will be a little better prepared for the "real world" than I was.
The Retirement Café
Retirement Planning for the Unwealthy
Tuesday, October 27, 2020
A New Approach for the Retirement Cafe Blog
Saturday, June 6, 2020
Life Cycle Economics and the Safety First Strategy
Well-read retirees will no doubt recognize the terms "Safety First" and "sustainable withdrawal rates (SWR)". "Safety First" refers to a retirement-spending strategy in which retirees first cover their essential retirement spending needs with assets that have no stock market risk and only then invest in a risky portfolio. SWR or "the probabilist school" as it is sometimes referred includes a strategy primarily based on stock market returns to fund both essential and non-essential retirement spending. The 4% Rule is a probabilist strategy.
The Safety First school is based on well-established Life-Cycle Economics theory that can be traced back to the early 1950s work of Franco Modigliani and his student, Richard Brumberg. Zvi Bodie, Jonathan Treussard and Paul Willen wrote a discussion paper for the Boston Federal Reserve entitled, "The Theory of Life-Cycle Saving and Investing" that is far more accessible than the relevant economics literature.[1] Still, a lot of us checked out of ECON 101 the first time the professor said, "marginal propensity to consume" so I imagine there are many of us who could use a little extra help.
The authors identify three principles for applying the life-cycle theory to financial planning.
Principle one tells us to focus not on the financial plan itself but "on the consumption profile that it implies.” Consumption equals income less savings during our working years and withdrawals from savings less health expenses in retirement.
Principle two says to view our financial assets as vehicles for moving consumption from one location in the life cycle to another. We can move consumption from our high-earning years to retirement by saving.
Principle three says a dollar is more valuable to an investor when consumption is low. A dollar of income is more valuable to us when we are unemployed, for example, than when we have a high-paying job.
Why should you care about life-cycle economics? It is a theoretical model of retirement finance and a decision-making framework that can serve as a guideline for answering our retirement finance questions. Life-cycle economics is based on Modigliani's observation that people make consumption decisions based on both how much wealth they have today and how much they expect to have in the future. In other words, they desire a consistent standard of living across their entire lifetime.
When a young worker saves some of her earnings in a retirement plan, she is deciding that she may need some of the wealth she could otherwise spend immediately after she retires. Her behavior is consistent with life-cycle economics in that she is considering not only her current spending needs but also deferring some of that spending to her retirement years when she may need it more.
Life-cycle economics can provide guidelines for far more than retirement finance questions. We can use it to decide how much to save, whether to buy insurance or how to finance the purchase of a home. The answer to each question can be different depending on our current position in the life-cycle. It will provide a different answer to the question of how much to save, for example, for a household in early adulthood, middle age, and late working years.
Now we have the basis of life-cycle finance. It's a set of guidelines, a "framework", for making financial decisions based on our stage of the human life cycle, our current financial situation, our expectations of future financial condition and, most importantly, science. Life-cycle economics tells us that our goal should be to maximize our happiness (utility) of consumption (spending) over our lifetime. This is a far different goal than maximizing total portfolio returns as the SWR strategy recommends.
We allocate our current wealth such that our standard of living will be consistent throughout our lifetimes in good times and bad. This provides a framework for making retirement finance decisions. As Bodie, Treussard and Willen state in their discussion paper,"The theory teaches us to view financial assets as vehicles for transferring resources across different times and outcomes over the life cycle."
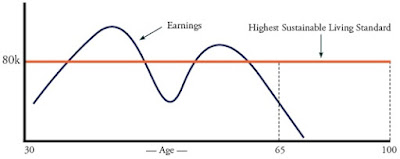
The following graph from Laurence Kotlikoff's esplanner.com website explains this process. The red line is the household's lifetime maximum sustainable living standard (consumption). The blue curve is lifetime earnings by age.
When earnings exceed the desired standard of living (the blue line is higher than the red), the household saves for future times when earnings may decline (blue line falls below the red). We smooth the peaks into the valleys until we find the highest "sustainable" amount we can spend (Kotlikoff's MaxiFi product makes this complex decision for you.[2])
We allocate our current wealth such that our standard of living will be consistent throughout our lifetimes in good times and bad. This provides a framework for making retirement finance decisions. As Bodie, Treussard and Willen state in their discussion paper,"The theory teaches us to view financial assets as vehicles for transferring resources across different times and outcomes over the life cycle.”
ADDITIONAL READING
REFERENCES
[1] The Theory of Life-Cycle Saving and Investing, Zvi Bodie, Jonathan Treussard and Paul Willen.
[2] Smarter Personal Financial and Retirement Planning Software | MaxiFi Planner, Laurence Kotlikoff.
[3] Risk Less and Prosper, Zvi Bodie and Rachelle Taqqu.
[4] The Future of Life Cycle Saving and Investing, Zvi Bodie, Dennis McLeavey, CFA, and Laurence B. Siegel.
[5] Safety-First Retirement Planning: An Integrated Approach for a Worry-Free Retirement, Wade Pfau.
Friday, April 17, 2020
Some Reading While We Wait
The video is a nine-minute YouTube explanation of a key economic issue, opportunity cost. It uses a Boston College football game as an example and features Nobel prize winners Robert Solow and Paul Samuelson.
I was also sent a link to Known Unknowns, which author Allison Schrager describes as "a newsletter that is coming to terms with uncertainty." The April 13 issue of Known Unknowns is about making sense of the market and features a discussion with economist, Zvi Bodie. The newsletter is free and you can subscribe (as I did) by supplying an email address at Allison's website, allisonschrager.com.
Don't stop with this issue of the newsletter, follow the links to other columns, like "better understanding of risk and uncertainty", and you will be well rewarded.
Peter Neuwirth provides an excellent column with outstanding writing at Medium.com. I thoroughly enjoyed his recent insightful essay, Making Smart Bets in the Age of COVID-19. The column leans heavily on the studies of Nassim Tabem. A key bit of wisdom can be found in the conclusion, "At the end of the day, we also believe that what is most important is that you be aware of the bets you are making as you are making them, that you become aware of the emotional and cognitive biases that may lead you astray, that you avoid all-in bets when you can, and that you make your life as anti-fragile as you can."
The April 16 issue of the Retirement Income Journal includes a column on the CARES Act by George A. (Sandy) Mackenzie. The author summarizes the column as "an updated summary of the Coronavirus Aid, Relief and Economic Security (CARES) Act, and then turns to the growing debate over how best to aid American small businesses—businesses with less than 500 employees—and their workers."
What am I reading in addition to these?
First, I am reading The Great Influenza: The Story of the Deadliest Pandemic in History by John M. Barry. It not only provides a detailed history of the 1918 "Spanish Flu" epidemic but of the political environment prior to World War I. It is fascinating and one can draw parallels to the current Covid-19 epidemic.
Lastly, unrelated to any of this, I'm reading Agency by William Gibson. Agency explores different timelines in which the last US election and Brexit turned out differently.
There's a lot of good stuff to read out there right now. I hope you find some of these enlightening. Stay safe.
Monday, March 30, 2020
The Question We Should Have Asked All Along
Do I believe there is an unacceptable risk that during my retirement the economy will not look like the recent past but will suffer from a major disruption (a pandemic, 70s-style low stock returns and high inflation, a depression, etc.) that should be considered in my retirement plan?When planning for retirement, we traditionally assume that the future will look a lot like the past. That isn't a great assumption but it often seems like the only guideline we have.
One of the problems with this approach is recency bias, the human tendency to overemphasize more recent data. Boomers who lived through the high inflation of the 70s think it could happen again; millennials who didn't can't imagine that inflation will ever exceed 3.5% again because it hasn't happened recently. We can't both be right.
Of course, neither cohort lived through the Great Depression so the concept of another depression and deflation doesn't typically creep into either of our thoughts. That doesn't mean it can't happen again, only that we can both suffer from a lack of experience and a failure of imagination.
This creeps into our retirement planning by ignoring a question that we should answer first but haven't bothered to do so in such a long time.
Why don't we ask? Because we intuitively believe that the risk of the future not looking like the recent past, "business as usual", is so low that it can be ignored. We believe that because it has been true for several decades. It's human nature. It's behavioral finance.
This isn't a yes or no question. The question isn't whether we believe the risk of a very different future exists but what probability we assign to it. We might, for example, believe that we probably won't experience a depression but assign a probability of 5% that we will. If 5% meets our risk tolerance threshold, we might decide in the spirit of taking the worst-case outcomes off the table that our retirement plan should address the possibility. If we're comfortable with a nineteen-in-twenty (95%) probability that it won't happen then we can build our retirement plan around the assumption that the future will look like the past.
The "D" word has become much more prevalent in the past month.
Economist, Laurence Kotlikoff, believes a depression is certainly possible.
"We have absolutely no game plan that will make any day of the next year look any better than today. Instead, we can expect each passing day to look worse thanks to all the layoffs and bankruptcies coming down the road."
He has posted a number of columns on the topic at his website that I urge you to read, perhaps beginning with "My Stock Tip –– Sell". (I also recommend a more recent Kotlikoff column in REFERENCES below.)
As one would expect when dealing with opinions about the future, other economists are not as convinced that a depression is imminent or the most likely outcome, though most I have spoken with lately don't rule it out and that is the important takeaway.
If a depression develops, then the best "risky portfolio" will not be stocks but, as Kotlikoff recommends, T bills are good, TIPS are safe. Inflation and long rates will go up. He also recommends shorting long Treasury bonds, though short sales can be challenging for the typical retired household.
Personally, I have no idea whether we are looking at a "business as usual" serious market decline and an 11-month recession or a depression. (An MIT Sloan study places the odds of a recession in the this year at a whopping 70%.) I only know that I now consider the risk of the latter as non-trivial and that I need to address that possibility in my retirement plan. You, of course, may not feel the same.
If you do now believe that a depression isn't out of the question then you may have the wrong retirement plan based on the assumption that the future always looks like the past.
Michael Finke, PhD, at The American College of Financial Services, writes an excellent piece entitled, "How Financial Plans Must Adapt to Market Crashes", at Advisor Perspectives. To quote Finke, "If the advisor decides not to course-correct because of faith that equity markets are going to “bounce back,” then they are guilty of subjecting their client to expectations that no longer match their current reality."
A key issue that you will need to address is your human capital. A well-paid 40-year old tenured university professor, for example, can take tolerate a lot more financial risk than someone who is already retired and has no human capital. Economist Zvi Bodie is the expert on this topic. If human capital is an unfamiliar term, a good place to start is Bodie's column entitled, "The Impact of Human Capital on Retirement Savings" or a little more detailed explanation entitled, "Retirement Investing: A New Approach".
Let me say again, I am not predicting a depression. I am only suggesting that it isn't an unreasonable outcome to consider in your retirement plan.
What to do now? If the risk of a severe economic downturn is one you feel you can tolerate, then stay the course with the traditional retirement plan advice. If, like me, you can't tolerate the risk of losing a funded retirement, then consider making changes to your portfolio that let you sleep at night. Since neither of us can predict the future, it largely boils down to your personal risk tolerance, risk capacity and human capital.
The first question we should have asked all along is whether we believe there is an unacceptable risk of a future that doesn't look like the recent past. Unfortunately, decades of good times taught us that the answer was always no.
I don't think that's a question we can simply ignore any longer.
REFERENCES
Group Testing Is Our Surefire Secret Weapon Against Coronavirus, a more recent post from Kotlikoff, recommends a strategy to "save potentially millions of lives and immediately restart the economy", exploring the inextricable link between the Covid-19 pandemic and our economic outlook.
Monday, March 16, 2020
How to Score Free Ben and Jerry's as a Retirement Planner
"You actually don't need to do anything", I replied.
"The market is down 20% but your portfolio is only down about 6% because a lot of your portfolio is in I Bonds and TIPS bonds. The annuity we purchased isn't subject to market risk, either, nor are your Social Security benefits, and those two pay most of your living expenses. The remainder is a small draw from your portfolio. So your spending hasn't been impacted and the market will eventually recover. So, why the seeds of panic?"
I assume the reply helped because the couple shipped me five quarts of Ben and Jerry's. (Who knew you could ship Ben and Jerry's?! Is this a great country or what?)[1]
The stock market has gone from raging bull to a bear market (roughly defined as a 20% decline or greater from a recent high) in just a few weeks. We recently experienced the longest bull market in history, so bear markets will come as a shock to many who have never experienced one but this is the way they work. The market drops precipitously. Life in the market seems grand and all of a sudden you’re trying to “catch a falling knife.”
I’d like to offer some perspective without the typical “stay the course” bromides that you can find anywhere, though I agree that’s good advice at this point.
First, you may have noticed that your risk tolerance has fallen as fast as the market. This is normal. During a roaring bull market, we have the feeling that we can tolerate a lot more risk than we feel we can tolerate during a bear market. It's human nature. Now is the time to reassess your risk tolerance, not during a sunny bull market. If you feel panic then your stock allocation is likely too high. Now is the time to adjust that for the next bear — you’re too late for this one.
Let's delve a bit deeper into why this couple is not panicking and I'm scoring ice cream big time.
Let’s say that before our mutual planning sessions a recently-retired couple had saved $1.5M in their two IRA accounts. The wife is quite risk-averse; the husband less so but strongly focused on ensuring that his wife is comfortable with their finances. Before planning, they owned mostly stocks and bonds but had no idea what they owned, why they owned it, or how much of each they owned. (I see this frequently, by the way.) Let’s guess they owned 50% equities and 50% bonds.
When the market fell 20%, their portfolio would have fallen about 10% or 11% with a 50% equity allocation (bond returns minus stock losses). Not nearly as frightening. That $1.5M would have been reduced to about $1.35M simply due to a less risky asset allocation.
But they had better news. To reduce risk to meet the wife’s risk tolerance, we had purchased a single premium income annuity (SPIA) with about $500K. The SPIA, when combined with joint Social Security retirement benefits, pays most of their living expenses and reduces the spending rate from their IRA’s to about 3% — a very sustainable draw.
A chart of 2020 year-to-date S&P 500 returns is fairly ugly right now, as you can see below from the chart of the Vanguard S&P 500 index fund VFINX produced at Morningstar.com. Hopefully, as a retiree, you weren’t 100% invested in stocks. If your portfolio were perhaps 50% stocks and 50% bonds, for example, before the bear, then your losses would be about 10% or 11%.
Also as a retiree, your investment horizon is a lot longer than one calendar quarter. So, let’s jump in Mr. Peabody’s Way-Back Machine and look at market returns from the beginning of this bull market, or right after the Great Recession that began in the fourth calendar quarter of 2007 with S&P500 market losses exceeding 50% by first quarter 2009. As the following chart shows, market returns since early 2009 have been fantastic.
(Also note that your recent losses occurred after an 11-year holding period, which belies the argument that stocks get safer the longer you hold them. The proper metric for retirement portfolio risk is terminal portfolio value, not annualized volatility. The range of possible portfolio value outcomes gets larger, not smaller, with time.)
I’m not going to suggest that you ignore the fear that comes with a precipitous market decline any more than I would ask you to stop touching your face or not see an elephant in your mind’s eye right now. There are some behaviors we simply can’t adopt.
Nor will I suggest, as many do, that “this is a perfect time to buy stocks”. Maybe it is and maybe it isn’t but market timing doesn’t work. Stocks are cheaper than they were last month but they may be cheaper still in the near future. Or not. No one really knows.
Interest rates are equally unpredictable. A year ago, many advisors would have recommended that retirees not purchase annuities given then historically low interest rates of a few percentage points. Overnight, rates are now near zero and that previously-purchased annuity looks pretty good. If you're trying to predict stock market prices or interest rates you're playing a loser's game.
What I do suggest is that you consider a longer perspective of market returns and realize that you were way ahead before you gave some back. Rebalance your portfolio once a year or so but only if your allocation is off by about 10% or more.
A reader emailed me not long ago to say that her advisor wanted her to sell stocks, incurring fees and taxes, because her asset allocation was off by a couple of percentage points. That’s pure folly. No one knows exactly what their asset allocation should be but it is a cinch that we can’t know it within a couple of percent.
According to CNBC[3], had you invested $10,000 in an S&P 500 index fund when the bull began in 2009, that investment would be worth about $45,800. Of course, you probably weren't 100% invested in equities so your portfolio return was lower but you’re still ahead of the game.
More importantly, because your portfolio probably wasn’t invested 100% in equities, especially if you follow my blog, your losses should be much less. My example retired couple lost only about 7% when the market fell 20% because we had set up an investment strategy that matches their risk tolerance. Not fun but certainly tolerable.
Purchasing a SPIA with some of your savings also removes market risk exposure and ensures lifetime income to pay your living expenses. That may help you invest the remainder of your portfolio more aggressively without causing too much angst. Remember when you hear that the S&P 500 has fallen X percent that a properly positioned portfolio has fallen only a fraction of that. (The same is true when the market rises X percent.)
Lastly, reconsider your risk tolerance and plan to make any changes to your target asset allocation that will help you sleep through these occasional bear market. It’s too late to do anything more about this one. I haven’t even looked at my portfolio since my annual review last December and have no plans to do so. If you, too, can reach that point then your planner has done a great job.
I’m pretty happy with mine.
REFERENCES
[1] How to Order Ben & Jerry’s Ice Cream Online | Ben & Jerry’s
[2] The market's 10-year run became the best bull market ever this month
[3] S&P 500 Return Calculator, with Dividend Reinvestment
Thursday, December 26, 2019
End-of-Year Thoughts on Retirement Planning
First, I would direct you to the post I wrote this time last year, My Year-End Review and Planning Regime, about steps you might want to take for a year-end review. As I warned then, don't bother being overly precise with your adjustments. This isn't an exact science.
I recall one reader whose adviser was suggesting she sell stocks and incur taxes just to correct an asset allocation by a percentage point or two. The process isn't that precise. It's impossible to know with any accuracy what your asset allocation should be unless you have a crystal ball that tells you next year's asset class returns. (If you do have a crystal ball, just allocate 100% of your assets to the asset class that will outperform all the others. But first, call me!)
I suspect that most retirees overthink the year-end adjustment process.
Next, President Trump signed the SECURE Act last week[1]. The age to begin RMD's was increased from 70.5 to age 72 beginning in 2020. However, "Americans who turned 70.5 years old in 2019 will still need to withdraw their required minimum distributions this year, and failure to do so results in a 50% penalty of their RMD", according to Jamie Hopkins, the director of retirement research at wealth management firm Carson Group.
Also, annuities can now be offered in 401(k) plans, though it may be a while before they actually become available. Thirdly, stretch IRAs are no longer available.[2]
Not everyone is convinced that the changes are dramatic. “The SECURE Act is a nice thing — anything we can do on a bipartisan basis in this day and age is something of value — but my sense is the changes in the act are really quite modest,” said Alicia Munnell, director of the Center for Retirement Research at Boston College and a columnist for MarketWatch.
I won't write yet another post on the topic because there are so many out there. I'll place some links in the references below and recommend that you start with Mike Piper's excellent piece at The Oblivious Investor.[3]
Wishing you a happy and prosperous 2020.
REFERENCES
[1] SECURE Act, downloads PDF.
[2] Hello SECURE Act, Good bye Stretch IRA | Ed Slott and Company, LLC, Ed Slott.
[3] Retirement and 529 Changes from the SECURE Act — Oblivious Investor, Mike Piper.
[4] The SECURE Act is changing retirement — here are the most important things to know -
MarketWatch.
[5] SECURE Act And Tax Extenders Creates Retirement Planning Opportunities And Challenges, Nerd's Eye View blog.
Friday, December 13, 2019
Evaluate Annuities as a Component of Your Retirement Income Portfolio
Purchasing a single-premium income annuity (SPIA) is the single most efficient way to maximize retirement income. According to Wade Pfau's Retirement Researcher Dashboard, a 65-year old couple with $100,000 today could spend about $5,750 annually from a life-only SPIA, $4,900 from a TIPS ladder, or $3,000 using the "4% Rule."[1] Of course, only the SPIA guarantees income for as long as you live but it also ends with no value. The TIPS ladder and portfolio can either be depleted prematurely or end up quite valuable depending on your longevity and investment results.
Sadly, it appears that the last company to offer CPI-linked annuities, The Principal, has stopped offering the product. A CPI-linked or "real annuity" also protected against inflation. But as Moshe Milevsky recently asked rhetorically, "Who says you have to get your inflation protection from an annuity?"
Nominal (not inflation-adjusted) annuities can still play an important role. Our goal isn't to ensure that inflation does not ravage our annuity income but to ensure that inflation doesn't ravage our retirement income. As Milevsky's comment suggests, the two need not necessarily be the same.
A frequent objection to lifetime income annuities is that they have no residual value after death, but the terminal net worth issue isn't straightforward. If we look at a simple SPIA in isolation from the remainder of a retirement plan, then clearly its terminal value will be zero. However, Pfau has shown that the most efficient way to generate retirement income for those with adequate resources is a combination of annuities and an investment portfolio. Furthermore, he has shown that purchasing an annuity can actually increase your terminal wealth by allowing your portfolio to grow more aggressively and by reducing sequence-of-returns risk.
For those of us with a bequest motive, our goal should be to maximize terminal wealth (net worth) from all assets whether or not an annuity is depleted. If an annuity provides no terminal value but allows a portfolio to grow larger, then the annuity will have done its job.
I wish I could convince more of you to consider annuities but, frankly, I understand why you might not.
First, unless your adviser also sells insurance, she isn't paid to sell annuities. In fact, your advisor may have a disincentive. An annuity takes away investable assets that do generate fees for most advisers. An uninspired and uncompensated adviser is unlikely to go out of his way to find you a great SPIA or to encourage you to purchase one.
The trick is to find an adviser who will provide unbiased recommendations regarding both investments and annuities and who also has a deep understanding of annuity contracts. That sounds like a big ask but I know a few that I trust. They're out there.
Even the simplest SPIAs are complicated. The contracts are not standardized so each has to be evaluated on its own merits. Pfau's recent book, Safety-First Retirement Planning[2], explains this in a chapter dedicated to different types of annuities and suggests questions you need to consider before purchase. You can also find these questions in an article by Pfau at Advisor Perspectives.[3]
Second, a SPIA purchase is a one-time, lump sum irreversible transaction. That's a tough sell for any product, financial or otherwise.
An annuity needs to be evaluated as a component of the entire retirement income plan and not as a standalone purchase. This means that an annuity contract is neither good nor bad but that it might or might not improve your overall plan.
It's like adding a new risky stock to a portfolio. Whether the portfolio's results are improved depends on how that stock's performance correlates with the existing portfolio of stocks. A stock can be a poor investment on its own but a welcomed addition to a portfolio.
The entirety of the retirement plan includes all household assets available for retirement funding including retirement accounts, taxable accounts, emergency funds, and even home equity. All of these may play a role in deciding to annuitize. You might, for example, elect to generate maximum income by purchasing a lifetime income annuity and then fund a bequest with your home equity.
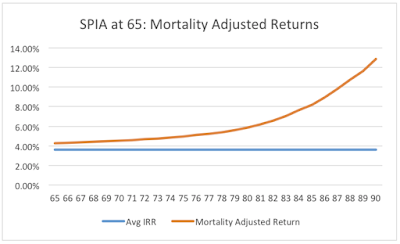
Should you decide to purchase an annuity a big question will be when to do so. An annuity is basically a bond portfolio with an insurance risk pool that provides mortality credits. These credits are provided to annuitants who live a long time by those that don't. Mortality credits increase over time but are minimal for younger annuitants.
The following chart created by actuary and retirement researcher, Joe Tomlinson shows the expected bond portfolio return for an annuity (blue line) and expected mortality credits by age (orange line) for a 65-year old female.[8] Keep in mind that the graph will change based on the annuitant's age, gender, marital status, and interest rates, so this chart is only for demonstration purposes.
Moshe Milevsky has studied the issue of when to optimally purchase annuities for nearly two decades and the advice is, well... complicated. He recently noted, however, that annuitizing too much too early seems highly suboptimal. This is because mortality credits are minimal at lower ages, annuity purchases are irreversible, many households have significant annuitized income from Social Security benefits, and annuity payments are exposed to inflation. Most households may be better off holding those assets in TIPS bonds for a while instead of annuitizing at the beginning of retirement. Laurence Kotlikoff's MaxiFi Planner is one of the tools available to help with the timing decision.[4]
Many retirees have strong reservations about the risk of an insurer failing. Tomlinson has also researched the number of annuities that have failed to deliver on their commitments historically. He found that very few have actually failed and those were from weaker insurers.[5] Purchase your annuites from a highly-rated insurer and you are very unlikely to encounter problems down the line.
Some express concerns about a massive failure of the insurance industry like the housing market crash in 2007. Tomlinson points out that insurance contracts are backed primarily by bonds and that there is no macroeconomic scenario in which a massive failure of the bond market wouldn't have an even worse impact on stocks.
While CPI-adjusted annuities may no longer be available, many insurers offer graduated-payment options or "Cost of Living Adjustments." Although these options suggest otherwise, they have no link to actual inflation. Regardless, researchers David Blanchett[6] and Joe Tomlinson[7] find that many annuities with a COLA option are currently priced more attractively than annuities with level payments, in other words, the insurers are accepting a smaller profit margin. The potential savings are worth investigating.
This raises the issue of how to calculate an annuity's expected value and compare it with other annuity options. This is a somewhat complicated process that Tomlinson explains in What Advisors Need to Know About Annuity Mortality Credits.[8] A retirement planner who knows his annuities should be able to perform this calculation for you.
The best annuity purchase you can make will be to defer your Social Security retirement benefits for as long as possible. If that doesn't provide an adequate floor of safe income, then you really should consider filling the gap with annuities. Integrated into your retirement plan, an annuity can solve a several retirement funding problems and mitigate those purchase objections.
To be clear, I don't think that everyone needs to purchase an annuity. Some households will have significant annuitized income from Social Security benefits. Wealthy households may not need them, although they may find the tax benefits attractive. But my guess is that a lot more households would benefit from annuities than purchase them.
I also encounter retirees who fear the stock market and have a strong preference for a dependable, budgetable "paycheck" each month. I generally advise them not to wait to annuitize. It isn't worth the angst to delay.
There are several common objections to life annuities but many of these objections can be mitigated if the purchase is properly integrated into the full retirement income plan and properly timed.
On a personal note, I have some challenges over the next few months that will make it difficult for me to post as regularly as I have in the past or to respond as quickly as I would like to your comments. Please bear with me and know that I will publish and respond to your comments at my first opportunity. Thanks.
REFERENCES
[1] Retirement Researcher Dashboard, Wade Pfau.
[2] Safety-First Retirement Planning, Amazon.com, Wade Pfau.
[3] Safety-First Retirement Planning, Advisor Perspectives, October 18, 2019, Wade Pfau.
[4] MaxiFi Planner software, Laurence Kotlikoff.
[5] How Safe Are Annuities?, Joe Tomlinson, Advisor Perspectives, August 14, 2012.
[6] Inflation-Linked SPIAs Are a Bad Deal, Advisor Perspectives, by David Blanchett, 5/20/19.
[7] Which Annuities Offer the Best Inflation Protection?, Advisor Perspectives, Joe Tomlinson
6/17/2019.
[8] What Advisors Need to Know About Annuity Mortality Credits, Advisor Perspectives, by Joe Tomlinson, 7/31/17.
Thursday, October 24, 2019
Two Pitfalls at Age 70½ That You'll Want to Avoid: Missed RMDs and the Tax Torpedo
In case you bail on this post after a couple of paragraphs, there are two very important things to know before you go. First, you are required to pay required minimum distributions on all employer-sponsored retirement plans, including:
- profit-sharing plans,
- 401(k) plans,
- Roth 401(k) plans,[1]
- 403(b) plans,
- 457(b) plans, and
- traditional Individual Retirement Accounts (IRAs),
- SEPs,
- SARSEPs, and
- SIMPLE IRAs.
If you have one or more of these accounts, heads up!
Second, the penalty for missing an RMD due date or withdrawing less than the correct RMD is 50% of the amount not withdrawn by the due date.[11] Your read that correctly — 50%. Your first RMD will be due by April 1st of the year after you reach age 70½. After that, RMDs are due on December 31st every year. Kiplinger has a calculator if you want to double-check your calendar math.[2]
OK, having been suitably warned, you can now feel free to bail at your own risk.
Congress created the IRA in 1974 with a pretty simple deal. Eligible workers under the age of 70½ could contribute to an IRA annually the lesser of $1,500 (a little over $7,000 in today's dollars) or 15% of compensation and not pay income taxes on these contributions or their investment earnings until funds were withdrawn from the IRA when we retired, which, at the time, seemed eons in the future.
Since withdrawals would be taxed at whatever the ordinary income tax rate (the rate we pay for work income) might be on the future date of the withdrawals, we were essentially allowed to defer income taxes on the amount of the contributions for four decades or so, at which time we would finally begin to pay income taxes on the original income and any earnings on that income. (The taxes were deferred, not avoided.)
This sounded like a pretty good deal and a lot of people jumped at it. Contributions totaled $1.4B in the first year. It was a good deal but after 44 years of tax deferral, shock of shocks, a lot of people don't want to pay the taxes now, either!
Go figure.
By 1987, Congress apparently realized that wealthier households might not need to spend the money in their IRAs so they created RMDs to discourage taxes being deferred forever. The goal of RMDs is to help ensure that most retirement account savings are actually spent during retirement, which was the original intent of Congress.
As I mentioned, the penalty can result from missing a deadline but also from miscalculating the RMD and withdrawing too little even if the deadline is met.
RMDs are calculated by dividing the balance of your IRA account on December 31st of the previous year by a factor that is based on your current age from IRS tables.[4] This is definitely the hard way.
You can Google a plethora of RMD calculators on the web that will make the calculations simpler. Your account custodian's[12] website probably has one. You will need to calculate the RMD for all retirement plans except Roth IRAs held with all custodians and withdraw their sum.
Easier still is to sign up for automatic RMD services with the investment companies that act as custodians for your accounts. Vanguard[8], Fidelity[7] and Charles Schwab[9], for instance, offer these services. They will withdraw the correct RMD by the correct deadline and eliminate that source of stress.
If you do make an error, Kiplinger explains that the error can be fixed and the penalty waived under certain circumstances.[3]
The second potential pitfall that can occur at age 70½ is directly related to RMDs but involves the taxation of your Social Security benefits. Social Security benefits are taxable at one of three levels based on your "combined income", which is essentially half of your Social Security benefit plus your other gross income and any tax-exempt interest.[5]
Based on this combined income, either none, 50% or 85% of your Social Security retirement benefits will be taxable. The 70½ problem is that RMDs might increase your income enough to make more of your Social Security benefits taxable, thereby increasing your total tax bill. This is a possibility, sometimes referred to as the "Tax Torpedo", that you should discuss with your tax planner, preferably well before you reach age 70½.
I receive a wide range of questions regarding RMDs and many are not what I would have expected. Here are a few of the more common queries:
I don't need to spend the RMDs I will withdraw. What am I supposed to do with the money?
This is one of those unexpected questions that I receive a lot and I have settled on the following response. When RMDs are withdrawn, the IRS essentially turns part of your retirement account balance into income that is taxed at ordinary income rates like income from a job. I suggest you consider the withdrawal a paycheck — it's going to be taxed as if it were. You can even have taxes withheld.
What would you do with this "paycheck?" Anything you want, the same as any other paycheck, except for putting it back into a tax-deferred retirement account.
The IRS doesn't care what you do with the withdrawn funds so long as you pay taxes on the withdrawal and stop deferring taxes on this amount by withdrawing it from the tax-deferred retirement account. You can spend the money, transfer it to a checking or savings account, or reinvest this part of your nest egg in a taxable account. Some of the custodians of your accounts, Schwab for example, will allow you to automate any of these actions.
Bottom line, if you don't want to spend this part of your nest egg, reinvest the remainder after taxes in a taxable account.
If I reinvest these withdrawn funds in a taxable investment account, will I not be taxed twice on my retirement savings?
No, you are finally being taxed for the first time on your tax-deferred contributions, possibly made decades ago, and their earnings. If you reinvest the withdrawn funds in a taxable investment account, you will be taxed on any future earnings on that account but you won't be taxed again on your retirement account contributions or earnings.
Can RMDs be avoided or reduced?
Maybe, if you start tax planning early enough to do Roth conversions, for example. Roth conversions are taxable, too, but you may be able to convert at lower tax rates, possibly even zero. This is another issue you will need to discuss with your tax planner but the closer you get to age 70½, the less likely you will be able to reduce RMDs.
As we approach age 70½, it is important to be aware of pending required minimum distributions and to avoid penalties for late or miscalculated withdrawals. The stress-free way to achieve this is to automate the RMD process with your retirement account custodian. They can ensure that your RMDs are accurately calculated for the accounts they hold, that the withdrawals are made on time, and that the funds you withdraw are used as you prefer.
We also need to be aware of the Social Security taxation implications. This is a fairly complicated issue that most retirees should discuss with a qualified income tax professional rather than trying to navigate it on their own.
Here's a brief to-do list:
1. If your account custodian is not one of the three I mentioned, contact yours and find out if they can automate your RMDs.
2. The automated RMD services typically require that you be at least 70½ years of age to make the request. Calculate the dates that you and your spouse will reach age 70½ here and stick reminders in your smartphone calendar to set up automated RMDs with your custodian(s) on those dates. If you have passed this age already, you can start the service immediately.
3. Start discussions with your tax advisor well before age 70½ if you hope to reduce RMDs or plan for the Tax Torpedo.
You can find much more detail on all of these topics at the references listed below.
REFERENCES
[1] Technically Roth 401(k)s, if they remain with your company after your departure or retirement, are subject to RMDs after age 70½. However, they can be rolled into a Roth IRA, which is not subject to RMDs during the owner's lifetime.
[2] When Do I Have to Take My First RMD?, Kiplinger
[3] Avoiding the 50% Penalty on Overlooked RMDs, Kiplinger.
[4] Required Minimum Distribution Worksheets | Internal Revenue Service
[5] How Worried Should I Be About the 'Tax Torpedo'?, Kiplinger.
[6] Benefits Planner | Income Taxes And Your Social Security Benefit | Social Security Administration
[7] Fidelity Investments Automatic Withdrawals - RMD
[8] Vanguard's Required Minimum Distribution Service
[9] Charles Schwab Automated RMD Service
[10] IRS Publication 590-B Cat. No. 66303U Distributions from Individual Retirement Arrangements (IRAs), page 35.
[11] A penalty will apply if your calculation is too low and you withdraw too little. Miscalculating and withdrawing an RMD that is too high won't generate a penalty because you can always distribute more than the minimum, though this may not be what you intend.
[12] An IRA custodian is a financial institution that holds your account's investments for safekeeping and sees to it that all IRS and government regulations are adhered to at all times. Retirement Tips: How to Choose the Best IRA Custodian, Investopedia.com
Saturday, September 28, 2019
The Prevalent but Problematic Probability of Ruin
Bengen's work gave us the 4% Rule, derived from the so-called probability of ruin. Probability of ruin, or p(ruin) for short, is the estimated probability that a retiree spending a fixed real dollar amount from a volatile portfolio will outlive her portfolio. Somehow, despite its many shortcomings, p(ruin) has become the most common metric in retirement planning.
The 4% Rule provides a "sustainable withdrawal rate" (SWR) that a retiree can supposedly spend from a volatile portfolio with a 95% probability of not outliving his savings. How much is the SWR? Bengen estimated a range around 4.4%. Wade Pfau, Michael Finke and David Blanchett[1] found that the SWR is currently closer to 3%, primarily due to a low-interest-rate regime. If they are correct, that would result in annual withdrawals nearly 32% lower than Bengen's estimate. That's quite a range.
Some question the implications of that research, notably Michael Kitces, but interestingly, William Bengen believes that valuations are probably important and that "Pfau may be on to something."
The Shiller CAPE 10 ratio[2], a measure of stock market valuation, was around 10 when Bengen's data series began in 1926 and today suggests a much higher market valuation of around 30. A higher CAPE 10 suggests lower future market returns and vice versa. Had the market return data series studied by Bengen begun when valuations were relatively high, the results may have suggested a lower SWR. (It is not uncommon for economics studies to improperly ignore initial conditions like market valuations.)
I will toss yet another monkey wrench into these analyses and note that both studies make assumptions about future asset returns so neither can be proven to be correct ex-ante. Still, Pfau et al. provides evidence that Bengen's SWR may be overestimated. This uncertainty is the essence of risk.
What are these shortcomings of p(ruin)? Let's start with p(ruin) being a one-dimensional measure of risk. By that I mean it estimates the probability (risk) of outliving a consumption portfolio, which I will define as a volatile portfolio of investments from which a retiree withdraws cash periodically to pay his bills, without measuring the magnitude of that risk.
Some research I'm currently coauthoring serves as an example. We compare two consumption-portfolio spending strategies. Each estimates a p(ruin) near 5%. On this basis, we would say that the two strategies are equally risky. However, when scenarios fail using the first strategy, the mean number of underfunded years is about 15. When scenarios fail using the second strategy, the mean number of underfunded years is about 21. The second strategy is riskier because when it fails, it leaves the retiree underfunded for 6 more years on average. This magnitude of risk isn't captured by p(ruin).
Another problem with p(ruin) is that it is based on a very limited sample of historical equity returns. Robert Shiller has reconstructed equity returns back to 1871, providing a little less than 150 years of data but this historical data contains very few unique long-term sequences of returns of 30 years or more that we need for retirement studies. We simply don't have enough data to draw statistically significant conclusions about the future probability of ruin. Many argue that only the more recent years of Shiller's historic returns are truly reliable.
Researchers have tried multiple strategies to get around this lack of data. Bengen used overlapping 30-year periods of returns. This strategy is flawed because the first and last years of the equity return time series are each used only once, the second and next-to-last twice, etc., while the returns in the middle of the series are included up to 30 times.
Another strategy is to generate 30-year series of returns by resampling, or randomly choosing returns from the entire historical data set with replacement. This strategy will provide results similar to the experience of the handful of available unique historical 30-year sequences of returns but doesn't generate "out-of-sample" series.
In other words, it assumes that the limited number of 30-year historical periods of data we have contain all of the information we will ever need to know about future market returns. It is more likely that the future will likely throw something at us that we have never seen before. Said a third way, our limited amount of historical long-term data series has very little predictive power. It can only tell us what might happen in the future if the future is very much like our limited past.
Let's focus now on a term I just introduced, "sequence of returns." The success or failure of a consumption portfolio is primarily a function of the sequence of the portfolio returns and not on the returns themselves. To quote BigErn at EarlyRetirementNow.com, "Precisely what I mean by SRR (sequence of returns risk) matters more than average returns: 31% of the fit is explained by the average return, an additional 64% is explained by the sequence of returns!"[4]
While we can generate realistic market returns from historical data using statistical methods like resampling, we cannot capture the most important characteristic of that data relative to portfolio ruin, the sequence of those returns. Resampling and most Monte Carlo models simply create random uniform sequences of returns and these are often quite unlike the few long sequences we observe from historical data.
This leaves two possibilities. One possibility is that the sequence of market returns is truly purely random as we most commonly model, in which case we have been extremely lucky not to have received a catastrophic sequence of returns over the past 150 years. Another possibility, and the one I favor is that sequences of returns are not purely random but are limited by market forces that we don't yet understand. In that case, we may never see catastrophic sequences of returns but our models are wrong.
I can't leave this topic without noting that consumption-portfolio failure doesn't require really bad negative returns. A long sequence of sub-par returns will do the trick. The worst-case series of 30-year returns beginning in 1964 that defines the 4% rule was simply a long period of mostly-positive but mediocre real returns.
Not long after the Great Recession, some SWR advocates were quick to note that the market had rebounded rather quickly, supporting the idea of a 4.5% SWR. While this is true, there are two important caveats. First, consumption portfolios recover much more slowly than a market index because we aren't spending from the market index. Second, the Great Recession was a three-year sequence and, as I note in the previous paragraph, portfolio failure typically results from long periods of mediocre returns and not short periods of negative returns.The Great Recession may not portend future portfolio failure for today's recent retirees.
Lastly, I think it is important that we consider the ability of humans to "internalize" probabilities. Clearly, there are some of us like Nate Silver, who can see a probability and intuitively interpret it. Most of us can't.
Most people tend to round small percentages to zero and large percentages to 100. The 2016 presidential election is a perfect example. On November 9, 2019, Nate Silver published a prediction that Trump had a 28.6% probability of winning the election and Hillary Clinton had a 71.4% probability. Many read this and concluded that Trump had no chance of winning, i.e., they rounded 28.6% to zero and 71.4% to 100%. When Trump won, they were outraged at Silver. I saw a poster at the Women's March saying, "I will never believe Nate Silver again."
The election was a one-time event and clearly not random. Silver's probabilities weren't based on counting who won past elections between Trump and Clinton. They represented Silver's belief that these were the odds and he believed that Trump's chances of winning were significantly greater than zero. It appears that many people didn't understand that.
This raises the issue of one-time events like a presidential election or your retirement. It's simple enough to look at a roomful of one hundred 65-year olds and say that a 4% Rule strategy means five of them will outlive their savings but it is impossible to say in advance which ive it will be. It is, therefore, difficult to internalize what 5% of retirees outliving their savings translates to your individual probability of failure.
(This is a poor analogy in one sense but I hope it makes the point. The 4% Rule says that 5% of 30-year periods will result in a failed portfolio, so if everyone in that room were 65 years old, they presumably all would go broke or none would. They will all experience the same future market returns.)
Your retirement differs from the 2016 election, although both are one-time events. We can use historical market data to count how often you might have succeeded in the past, given some withdrawal rate. The problem is that we don't have nearly enough of that data. Even if we did, we could only predict how many retirees would fail and not whether you would be one of them.
The point of our ability or inability to intuitively understand probabilities is that many people will round a 5% chance of ruin to zero and feel perfectly safe, while others (like me) will feel that a 1-in-20 chance of ending up destitute in their dotage is completely unacceptable. In either case, p(ruin) is frequently problematic because of our inability to intuit it.
There are a couple of other shortcomings of p(ruin) that I will briefly mention in conclusion. Many argue that no retiree would ever do what the 4% rule requires, that is, to continue to spend the same amount from a consumption portfolio even when it is obviously failing. First of all, I would note that if the retiree doesn't do this, then the 4% Rule is not predictive at all because the retiree isn't adhering to the strategy but I also have anecdotal evidence that there are rational reasons a retire would continue spending the same amount.
At some point, a retiree with a failing portfolio will reach an amount of spending that is necessary to meet non-discretionary expenses and spending too much to pay necessary expenses will be the rational response even if it will undoubtedly lead to portfolio depletion in the near future (see Why a Rational Retiree Might Keep Going Back to that ATM).
If the 4% Rule says I can spend no more than $1,000 or else I will probably go broke in the near future but my necessary expenses total $1,500, I will spend the $1,500. In this scenario of continued fixed spending, portfolio behavior is either chaotic or behaves chaotically and it doesn't matter much which (see Retirement Income and Chaos Theory).
Economist, Laurence Kotlikoff believes the 4% Rule estimates both the wrong amount to save and the wrong amount to spend compared to an economics approach. He explains it better than I could in The 4% Retirement-Asset Spend-Down Rule Is Rubbish.[5]
Lastly, probability of ruin is a number that we intentionally try to make as small as practical. It's a measure of "tail risk", or the area of low-probability outcomes of a model. Nassim Taleb, in testimony before Congress no less[6], stated that "the more remote the event, the less we can predict it." Taleb goes on to say, "Financial risks, particularly those known as Black Swan events cannot be measured in any possible quantitative and predictive manner; they can only be dealt with non-predictive ways." But, predicting unlikely events is precisely what p(ruin) purports to do.
The 4% Rule has achieved cult status to the extent that I hear retirees with virtually no other knowledge of retirement finance casually refer to it as if it is a universal law. It is not. It is a questionable but unfortunately prevalent retirement finance metric.
A better approach is recommended by life-cycle economics (see, for example, Risk Less and Prosper by Zvi Bodie), sometimes referred to as "safety-first." The safety-first strategy is to assume that portfolio failure is a (perhaps) small — Taleb would say unquantifiable — probability of an unacceptable outcome. It deals with the risk of portfolio depletion "in non-predictive ways." The retiree is encouraged to plan for an acceptable standard-of-living in the event of that outcome without having to roll the dice and simply hope the future looks a lot like the past.
REFERENCES
[1] The 4 Percent Rule Is Not Safe in a Low-Yield World , Michael Finke, Ph.D., CFP®; Wade D. Pfau, Ph.D., CFA; and David M. Blanchett, CFP®, CFA.
[2] Shiller PE Ratio, Multpl.com.
[3] Online Data, Robert Shiller, Yale Economics.
[4] The Ultimate Guide to Safe Withdrawal Rates – Part 15: More Thoughts on Sequence of Return Risk, EarlyRetirementNow.com.
[5] The 4% Retirement-Asset Spend-Down Rule Is Rubbish, Laurence Kotlikoff, Forbes.com.
[6] The Risks of Financial Modeling: VAR and the Economic Meltdown, House Subcommittee on Investigations and Oversight, GPO.
Thursday, August 15, 2019
Why Can't We Stop Pfishing?
By close of business the following day I had developed a full appreciation of the threat because I had unwisely clicked on a link in an Instant Message and unwittingly handed my employee login credentials to a hacker, something I had been told not to do just hours before. IT's "clean-up" process took two days, though I suspect that was a form of punishment, and during that time I wore the scarlet letter of being cut off from the rest of the company that functioned entirely around AOL Mail and Instant Messaging.
What a dunce. Lesson learned.
AOL finally put a huge dent in the phishing attacks by implementing two-factor authentication (2FA) for all employees, as I described in those previous posts, except that in 1997 we used hardware tokens because there were no smartphones.
Having dedicated my last two posts, You're Responsible for Your Own Online Security and How to Secure Your Online Financial Accounts, to securing online financial accounts, I realize my retirement finance blog has taken on a computer-geek air of late. My rationale is that retirement finance is primarily about dealing with risk and cyber security is a huge component of financial risk.
Malwarebytes.com describes phishing attacks as follows.
"Phishing is the crime of deceiving people into sharing sensitive information like passwords and credit card numbers. As with real fishing, there's more than one way to reel in a victim, but one phishing tactic is the most common. Victims receive a malicious email (malspam) or a text message that imitates (or “spoofs”) a person or organization they trust, like a coworker, a bank, or a government office. When the victim opens the email or text, they find a scary message meant to overcome their better judgment by filling them with fear. The message demands that the victim go to a website and take immediate action or risk some sort of consequence."The term "phish" comes from fishing. A hacker dangles some bait in front of you in the form of a disguised hyperlink in an email or text message and hopes you will click on it hook, line and sinker.
Phishing attacks can be implemented with text messages, email, or even phone calls. It is actually a "social engineering" attack because rather than relying on technology to steal your vital information, it relies on you giving away that information in a moment of fear, confusion or just complacency.
Some people provide their sensitive information over the phone in spite of knowing that no bank, brokerage or government office like the Social Security Administration is going to call, text or email you and ask for your login credentials. The IRS does not announce an audit in an email.
Others click on a hyperlink in an email or text message because they believe they know the sender or because the link looks familiar or harmless. It isn't difficult for a hacker to change an email sender's address, using an attack known as "spoofing." You cannot trust an email's source simply by looking at the sender's email address or a phone call's source by checking Caller ID.
A lot of people who should know better get hacked by phishing attacks. It's a highly effective strategy.
Cyber security firm, CSO, lists three infamous phishing attacks.
- Perhaps one of the most consequential phishing attacks in history happened in 2016 when hackers managed to get Hillary Clinton campaign chair John Podesta to offer up his Gmail password.
- The "fappening" attack, in which intimate photos of a number of celebrities were made public, was originally thought to be a result of insecurity on Apple's iCloud servers, but was in fact the product of a number of successful phishing attempts.
- In 2016, employees at the University of Kansas responded to a phishing email and handed over access to their paycheck deposit information, resulting in them losing pay.
(Note to political parties: Why are you sending unencrypted sensitive information over email systems like GMail when you can create a free, encrypted account at CERN's Proton Mail or spend a few bucks to encrypt your own mail server? More importantly, why are you saying things in an email that you wouldn't want the world to share? Emails never die. Your stupidity will be on the web forever. This is not the way you want to go viral.)
My goal is to help you protect yourself and your wealth from phishing attacks (if political organizations haven't figured out how by now then I have little hope for them in cyberspace).
Because phishing attacks are social engineering attacks that depend on tricking you, your diligence is the best protective measure. Think twice — no, make that three times — before you click on any link in an email or text message.
Check the context. My friend, Lex, send me lots of emails, text messages and messaging app thoughts. I normally click on all of his links but when I recently received an email from him that contained nothing but a hyperlink, I deleted it. It would be very unusual for Lex to send me a link with no explanation.
Needing no further clues, I checked the email's CC list and noticed it was quite long and included no one that I know. Not a confidence-building sign.
If I have any doubt that a link I receive is not legitimate, I will contact the sender and ask if the email or message was really from them but it is critical to contact them through a different channel and not by replying to the message. If the link really is phish, then replying may simply be me asking the hacker if he is legit. He'll probably say yes. If the link arrives in an email, for example, call or text the sender, instead.
When I receive an email or text message regarding the status of a credit card account, I visit the card's website without clicking on the link.
It's quite easy to make a link look like a legitimate website when it actually points to a hacker's own malicious website. It's also quite easy to make that website look like Chase Bank's website, for example, and encourage you to "login" at the fake website and thereby hand your login credentials to the hacker.
Most email systems and websites allow you to view the actual link by hovering your mouse over the hyperlink. The underlying link will appear. Read the actual link closely to detect small changes that indicate you might not land where you expected.
You may find, for example, that a link that appears to point to theRetirementCafe.com (my website) actually points to theRetirmentCafe.com, which could belong to anyone. Notice the subtle misspelling. Hover your mouse over each of these links and, depending on your browser, the actual destination hyperlink will show up somewhere on your screen.
Some anti-virus and anti-malware software also incorporates anti-phishing features. Check your software's website to know for sure. Still, it won't replace your own diligence in examining hyperlinks sent to you before clicking on them.
Why are phishing attacks still so successful though we've been exposed to them since the late 1990s? They prey on our fear, complacency, and familiarity. It should be really easy to always say, "I'm not 100% sure this is a legitimate link so I'm just not going to click it" or "no legitimate business would ask me to provide sensitive information through an email or a phone call," yet it remains a successful hacking strategy.
One last question you might ask yourself is what would happen if I don't click this link? If it is important, the sender will surely try other ways to reach you, even if it's a friend just making sure that you saw the link she sent to her latest baby pictures.
Phishing attacks aren't the only cyber threat to your wealth but they are one of the most common and they are very effective. The best way to protect yourself is to treat any link sent to you as a potential threat. Never click on them without stopping to think about possible bad outcomes. Err on the side of avoiding the pfisher. If you're not certain, don't click.
Tuesday, August 6, 2019
How to Secure Your Online Financial Accounts
You may be thinking, "That's a lot of trouble. In the unlikely event that my account is hacked, the financial services company will reimburse me." I think that's a mistake for a few reasons. First, even if the company covers your losses, recovering from the fraud is unlikely to be a pleasant experience. Second, if you don't meet the company's security requirements spelled out clearly on their websites, you might not be covered by their online fraud guarantee, at all. Do you want to take that risk with your savings?
My goals for this post don't include boring you to tears, though that is certainly a risk when one explains technology to people who just want things to work. The truth is that Internet passwords don't work. We need a very different solution for securing online access but unless and until we get that, we have to work with what's available.
One of my goals is to help you avoid losing your hard-earned wealth to online fraud. A second goal is to help you avoid the long, painful process of recovering from online fraud when recovery is possible — you'll find it much easier to stop fraud before it happens than to tidy up afterward. And, my third goal is to keep you from running afoul of requirements that might preclude those "100% online fraud guarantees" offered by financial services companies. I used to refer to them as "online financial services companies" but now almost all of them are.
I warn you up front that some of these measures can be complicated to implement and that they will complicate your financial life a bit. It won't be as easy for you to access your online financial services but it should be a lot more difficult for a thief to do so.
And finally, before diving into security measures, be aware that many online services offer different levels of security that you can implement depending on how much set-up work you are willing to do and how much inconvenience you will tolerate to achieve greater security. You can improve security significantly with stronger passwords, for example. With more work and complexity, you can greatly improve on long-password security by adding two-factor authentication. You will need to decide if the extra security is worth the effort.
You might also think, "This is way too difficult. I'm just going to avoid online access to my accounts altogether."
While this might be achievable in some limited way, it will preclude most investment opportunities. I asked Fidelity Investments if it is possible to open an account with no online access. They thought I had lost my mind. And, should you decide to simply not set up the online access, a thief might well do it for you.
Wade Pfau and the gang at RetirementResearcher.com are seeking volunteers for a research project called the Retirement Income Style Awareness,™ (RISA™). Please consider following this link to the survey. Participants will be able to get results from the survey in the fall.
First, if your computer, smartphone, or tablet is compromised, no other security process can be trusted. If someone installs a keylogger on your computer, for example, that person can watch you type in your log-in credentials from half a world away and it won't matter what other security measures you take, they're looking over your shoulder. Run anti-malware software on your computer and only download smartphone apps from your apps store. This step is essential. There are several excellent free anti-malware products for computers. I like Avast for Mac[1]. Windows Defender[2] generally gets high marks, as well.
Next, you probably have a lot of sensitive information on your smartphone. Many services will use your phone to reset your password, for example. A thief doesn't need to learn your password if she can more easily reset it. Actually, a thief doesn't need to physically steal your phone. He may be able to illegally "port-out" your phone number and receive all your phone calls and text messages. Your smartphone is a key to your online security whether or not you intended it to be.
You need to keep that key beyond the grasp of hackers. Bite the bullet and change your lock-screen passcode to at least 8-digits.[3] (Are you still using four digits?) This step is also essential. I'd recommend avoiding lock-screen patterns on Android phones.
For many financial services companies, the use of "third-party aggregators" like Mint.com, Fidelity Fullview and Vanguard Portfolio Watch will violate your guarantee of fraud protection. Charles Schwab explicitly states next to the button to enable these services that they invalidate your guarantee. Stop using them. This is an essential step. You can go to the aggregator websites and turn off the feature but you can also change the passwords on all your financial services accounts (which you probably should do, anyway) and simply not update them at the aggregator website. If your financial data still shows up at your aggregator site, you know you're not finished. The aggregators will no longer have access to your data and you will no longer be in violation of the terms of your guarantee.
Creating strong passwords is an essential step. Make passwords to all your sensitive online accounts at least 12 random characters long. Use upper and lower case letters, numbers and special characters as allowed by the website. Here's an example: Wt4e-7B13^qS. As the saying goes, the best password is the one you can't remember. It has been estimated that an 8-character password can be cracked in hours, nine characters in months, and 12-character passwords in hundreds of years with a brute force attack. If your password contains recognizable words, a dictionary attack can be even faster.
Don't reuse passwords. This is essential because cracking one of your passwords compromises every other account using that password. Every sensitive account should have its own.
Never share your password with anyone other than a spouse on a joint account. That will almost certainly invalidate your online fraud protection. If you want an advisor or a spouse to have access to your individual accounts, grant that authority explicitly by filing the appropriate paperwork with your financial services companies instead of going through the "back door" of sharing your passwords. Recognize the risk you're taking by doing this and consider sharing "read-only" access and not authority to transact in your account.
If you write them down, store the list of passwords in a secure location and hide a backup in a different physical location. The next step isn't essential but I find it helpful. I use a password manager to both create random passwords and store them. LastPass, Dashlane, and 1Password are perhaps the best known and you can access passwords from your computer, smartphone, and tablet.
The next level of security (and complexity to implement and use) beyond strong passwords is two-factor authentication. 2FA is perhaps not as essential as strong passwords but many experts would disagree. I consider it mandatory for my accounts but I also recognize that it is complicated for a "non-techie" to understand and implement. I can imagine that most will consider it too complex and that's a shame because it is a huge step up in security.
In essence, 2FA provides a second password that changes every minute and can only be read from an app on your smartphone (or a dedicated hardware token[4]). Unless a thief has access to your smartphone, she can't log in to your account even if she knows your password.
2FA is now offered by most, though not all, financial services websites. I even use 2FA at social media websites and on my email accounts. Two Factor Auth[5] provides a list of websites that support 2FA and PCMag.com[6] explains how to use many of them.
I have found that customer service departments of financial services companies will walk you through implementing 2FA over the phone if you ask and it only takes a few minutes. This is far and away the easiest way to implement 2FA on your account.
There are several ways in which 2FA can be implemented. The passcode can be sent to you in an email, sent to your phone in a text message (SMS), delivered by a voice phone call, or created by an app on your phone. If your financial services company offers a choice, the app approach (or a hardware token) is the safest.[7]
Some websites, like TreasuryDirect®, will email a one-time password (OTP) as a second layer of authentication after you enter the correct password. A lot of people know I can be reached at JDCPlanning@gmail.com and that's the first place a hacker might search for my one-time password. It would be harder for a hacker to intercept my OTP if I have it sent to say, dog73202@gmail.com, which doesn't identify me.
If any of your accounts use 2FA by sending an email, consider setting up an email account with a random name solely to receive 2FA passcodes. Set up a notification in that email account to alert you anytime you receive an email.
Many websites have a "password recovery" process that will reset your password if you answer security questions like "What was your high school mascot?" It makes no sense to go to all this trouble to secure a password when someone can "recover" your password by answering these security questions after reading your social media posts or by Googling your name.[10]
(I checked my password recovery questions on an email account I use for junk and found that that a hacker would need to either spend hundreds of years guessing my password or simply guess the name of my favorite band to gain access to my account.)
I make up unrelated answers to these questions and store both the questions and the answers with my passwords. For example, I might choose the question "What was your school mascot?" ("Eagles" is a good guess for a hacker.) I might enter "bookbinder" as the answer.
Thieves can sometimes illegally "port-out" your mobile phone number to theiro phone and the only indication you will get that this has happened is that your phone will stop working. They'll receive your text messages and phone calls so they'll intercept any one-time passwords sent by either of those methods. Furthermore, many online accounts will allow you or a thief to recover your password by texting or calling your phone and the thief is now the recipient of both of those. You may have the physical phone in your hand but all of your voice calls and text messages will now go to the thief's phone.
To illegally port-out your phone number, a thief only needs some basic name and address information about you and a PIN that is set up at your wireless carrier's website. Better beef-up the security of wireless carrier passwords and PINS with your wireless carrier. Krebs on Security tells you how.
Log on to your wireless carrier online account and make sure your PIN isn't something obvious like "1234" or the last four digits of your social security number. Use a strong password on your wireless carrier's website. I added 2FA to mine. Otherwise, the fraudster can hack into your wireless carrier account and change that PIN. Your smartphone, one way or the other, is the key to much of your online security. If it is lost or stolen, take action immediately.[8,9]
Since this all began with a reader's comment regarding security at TreasuryDirect®, let's look at how we might secure accounts there.
To log on to a TreasuryDirect® account, a thief will need your account number, a password for that account, an email address to which TreasuryDirect® will send a one-time passcode each time we attempt to log on, and that one-time passcode.
First, create a random password at TreasuryDirect® that is at least 12 characters long. Then, create unrelated answers to password recovery security questions at TreasuryDirect®, as described above.
Create a new email address with a random name and direct TreasuryDirect® to send one-time passwords there instead of sending it to your public primary email address. Secure the email account with a long, random password.
Now, a hacker will need to learn your TreasuryDirect® account number, hack its long random password, figure out what e-mail account you have told TreasuryDirect® to send your one-time password, and hack that e-mail's long random password to learn your OTP. If he tries to hack your TreasuryDirect® account using password recovery, he will need to know that you told TreasuryDirect® that your father was born in the city of banjo.
I believe any web-based service is hackable but a thief could probably find an easier way to steal money than this.
If you only install anti-malware software on your computer and improve your passwords, you will greatly enhance your online security. If this seems overwhelming, start by improving all of your passwords on financial services company websites and do more later.
You can download a checklist in Word to organize your security enhancement project. I included a sample using a Charles Schwab account. Click the link to see the document, then click download to save a copy.
This is the world we live in. Practically all financial services companies have an online presence with fraud guarantees provided only if the company considers that you have adequately protected your login credentials.
I realize that most readers will find this all quite complicated even with the links I have provided but this is your retirement savings we're trying to protect here and i4 your security doesn't meet the standards of financial services companies, their "100% online fraud guarantee" might not be available to you. Follow these steps and you are far less likely to ever need to recover from online fraud or rely on a fraud protection guarantee.
Some readers are having problems posting comments anonymously. Please feel free to email comments to JDCFinance@gmail.com and request that I post them anonymously.
REFERENCES
[1] Avast for Mac
[2] Windows Defender, Microsoft.
[3] Change Your IOS Passcode. or Change Your Android Passcode for Android.
[4] Some financial services companies will provide, often for free, a hardware "token" to generate the 2FA passcode instead of using your phone. See Protect Your Investment Accounts With A Security Token.
[5] Two Factor Auth list of 2FA supported websites.
[6] Two-Factor Authentication: Who Has It and How to Set It Up, PC magazine.
[7] This is why you shouldn’t use texts for two-factor authentication, TheVerge.com. Major SMS security lapse is a reminder to use authenticator apps instead, TheVerge.com.
[8] If your iPhone, iPad, or iPod touch is lost or stolen.
[9] Find, lock, or erase a lost Android device, Google Help.
[10] Time to Kill Security Questions—or Answer Them With Lies, Wired.
[11] This is why your six-digit iPhone passcode isn’t secure, BGR.com.